Given:
Cameron has 21 coins in his pocket, all of which are dimes and quarters.
Let, x be the number of quarters and y be the number of dimes.
The total cost is 315 cents.
The equations are,
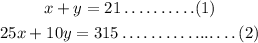
Solve the equation,

Put the value of y in equation (1),

Thus, the number of quarters are 7 and dimes are 14 .