We have to find the 80% confidence interval for a population proportion.
The sample size is n = 362 and the number of successes is X = 54.
Then, the sample proportion is p = 0.149171.
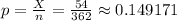
The standard error of the proportion is:
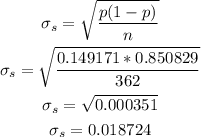
The critical z-value for a 80% confidence interval is z = 1.281552.
Then, the lower and upper bounds of the confidence interval are:
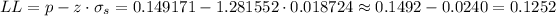
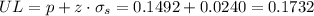
As the we need to express it as a trilinear inequality, we can write the 80% confidence interval for the population proportion (π) as:
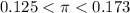
Answer: 0.125 < π < 0.173