176.4
Step-by-step explanationas the triangle are similar we can set a proportion
Step 1
find the YZ value
a) let
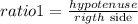
so,for triangle XZW
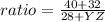
and for triangle XYV
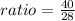
as the ratios are equal, we can set a proportion
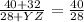
b) now,solve for YZ

so
YZ=22.4
Step 2
find the length of the side WZ
a) let
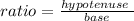
hence
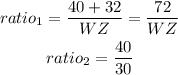
set the proportion and solve for YZ
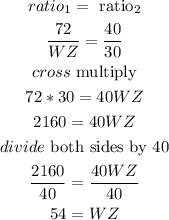
Step 3
finally, find the perimeter of triangle XZW
Perimeter is the distance around the edge of a shape,so
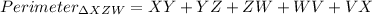
replace and calculate
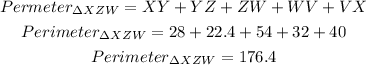
therefore, the answer is
176.4
I hope this helps you