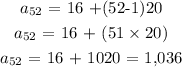Question

Find the 52nd term.16, 36, 56, 76,…

Answer 1

`\text{ a}_(52)\text{ = 1,036}`

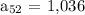
Step-by-step explanation:

Here, we want to find the 52nd term of the sequence

What we have to do here is to check if the sequence is geometric or arithmetic

We can see that:

`\text{ 36-16 = 56-36=76-56 = 20}`

Since the difference between the terms is constant, we can say that the terms have a common difference and that makes the sequence arithmetic

The nth term of an arithmetic sequence can be written as:

`\text{ a}_n\text{ = a +(n-1)d}`

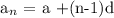
where a is the first term which is given as 16 and d is the common difference which is 20 from the calculation above. n is the term number

We proceed to substitute these values into the formula above

Mathematically, we have this as:

`\begin{gathered} a_(52)\text{ = 16 +(52-1)20} \\ a_(52)\text{ = 16 + (51}*20) \\ a_(52)\text{ = 16 + 1020 = 1,036} \end{gathered}`