Question

How does g(t) = 4t change over the interval t = 3 to t = 4?

Answer 1

The function
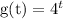`\text{g(t)} = 4^t` over the interval is that g(t) increases by a factor of 4

Finding the change of the function over the interval

From the question, we have the following parameters that can be used in our computation:

`\text{g(t)} = 4^t`

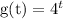
The interval is given as

From t = 3 to t = 4

The function is an exponential function

This means that it does not have a constant average rate of change

So, we have

`\text{g(3)} = 4^3 = 64`

`\text{g(4)} = 4^4 = 256`

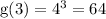
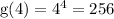
Next, we have

Change = 256/64

Evaluate

Change = 4

Hence, the change of the function over the interval is that g(t) increases by a factor of 4

Answer 2

Over the interval t = 3 to t = 4, g(t) increases.

The increasing factor (f) is computed as follows:

`f=(g(4))/(g(3))`

where g(4) is g(x) at t = 4, and g(3) is g(x) at t = 3. Substituting with the formula of g(t) and evaluating each expression, we get:

`\begin{gathered} f=(4^4)/(4^3) \\ f=(4\cdot4^3)/(4^3) \\ f=4 \end{gathered}`

Then, g(t) increases by a factor of 4