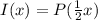When we're dilating a line, we can either multiply the function value by a constant
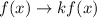
or the argument of the function

Since the y-intercept of both functions is the same, then the multiplied quantity was the argument of the function.
We want to know the constant associated to the transformation

We have the following values for both functions
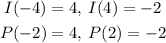
For the same y-value, we have the following correlations
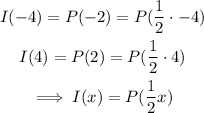
and this is our answer.