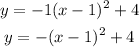Question

Write the equation of the function in the graph.. Please show all of your work so i can understand

Answer 1

The vertex form of a parabola is:

`y=a(x-h)^2+k`

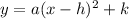
where (h, k) is the vertex of the parabola and a is some constant.

From the graph, the vertex is located at (1, 4), that is, h = 1 and k = 4.

Substituting with these values and the point (0, 3), we get:

`\begin{gathered} 3=a(0-1)^2+4 \\ 3-4=a(-1)^2 \\ -1=a\cdot1 \\ -(1)/(1)=a \\ -1=a \end{gathered}`

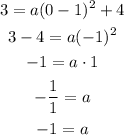
Then, the equation of the function is:

`\begin{gathered} y=-1(x-1)^2+4 \\ y=-(x-1)^2+4 \end{gathered}`