Question

The floor of a shed has an area of 80 square feet. The floor is in the shape of a rectangle whose length is 6 feet less than twice the width. Find the length and the width of the floor of the shed. use the formula, area= length× width The width of the floor of the shed is____ ft.

Answer 1

Given:

The area of the rectangular floor is, A = 8- square feet.

The length of the rectangular floor is 6 feet less than twice the width.

The objective is to find the measure of length and breadth of the floor.

Consider the width of the rectangular floor as w, then twice the width is 2w.

Since, the length is given as 6 feet less than twice the width. The length can be represented as,

`l=2w-6`

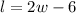
The general formula of area of a rectangle is,

`A=l* w`

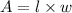
By substituting the values of length l and width w, we get,

`\begin{gathered} 80=(2w-6)* w \\ 80=2w^2-6w \\ 2w^2-6w-80=0 \end{gathered}`

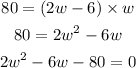
On factorizinng the above equation,

`\begin{gathered} 2w^2-16w+10w-80=0 \\ 2w(w-8)+10(w-8)=0 \\ (2w+10)(w-8)=0 \end{gathered}`

On solving the above equation,

`\begin{gathered} 2w+10=0 \\ 2w=-10 \\ w=(-10)/(2) \\ w=-5 \end{gathered}`

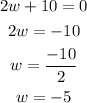
Similarly,

`\begin{gathered} w-8=0 \\ w=8 \end{gathered}`

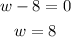
Since, the magnitude of a side cannot be negative. So take the value of width of the rectangle as 8 feet.

Substitute the value of w in area formula to find length l.

`\begin{gathered} A=l* w \\ 80=l*8 \\ l=(80)/(8) \\ l=10\text{ f}eet. \end{gathered}`

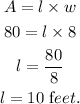
Hence, the width of the floor of the shed is 8 ft.