ANSWER
The output rate for the Hernandez family was 15 L/hr and for the Fox family was 35 L/hr.
Step-by-step explanation
To solve this problem, we have to create a system of two simultaneous equations.
Let the output rate of the Hernandez family sprinkler be h.
Let the output rate of the Fox family sprinkler be f.
The product of the rate and the time used is equal to the output:
![\text{Rate}\cdot\text{time}=\text{output}]()
We have that the combined total output for both sprinklers is 1275 L, which means that:
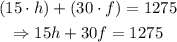
The sum of the two rates is 50 L/hr, which means that:
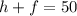
Now, we have a system of two simultaneous equations:
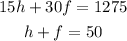
Solve the equations by substitution.
Make h the subject of the formula in the second equation:
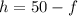
Substitute that into the first equation:
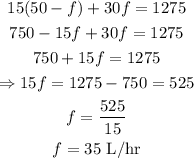
Recall that:
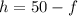
Therefore, we have that:
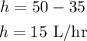
Hence, the output rate for the Hernandez family was 15 L/hr and for the Fox family was 35 L/hr.