Question

For each ordered pair, determine whether it is a solution to the system of equations. 7x - 4y=8 -2x+3y=7 Is it a solution? (x, y) Yes No (0, -2) a (-9,-6) (4,5) (7.7)

Answer 1

7x - 4y = 8 (eq. 1)

-2x + 3y = 7 (eq. 2)

Isolating y from equation 1:

-4y = 8 - 7x

y = 8/(-4) - 7/(-4)x

y = -2 + 7/4x

Isolating y from equation 2:

3y = 7 + 2x

y = 7/3 + 2/3x

Given that the slopes of the equations are different, then there is a solution, which can be found as follows,

`\begin{gathered} -2+(7)/(4)x=(7)/(3)+(2)/(3)x \\ (7)/(4)x-(2)/(3)x=(7)/(3)+2 \\ \frac{^{}_{}7\cdot3-2\cdot4}{4\cdot3}x=(7+3\cdot2)/(3) \\ (13)/(12)x=(13)/(3) \\ x=(13)/(3)\cdot(12)/(13) \\ x=4 \end{gathered}`

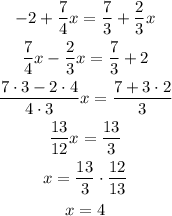
Replacing x = 4 into one of the equations, we get:

`\begin{gathered} y=-2+(7)/(4)x \\ y=-2+(7)/(4)\cdot4 \\ y=-2+7 \\ y=5 \end{gathered}`

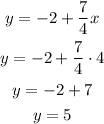
The solution is (4,5)

To check if an ordered pair is a solution, we have to replace the x-coordinate and the y-coordinate of the pair into the equation, as follows:

(0, -2)

7(0) - 4(-2) = 8

8 = 8

-2(0) + 3(-2) = 7

-6 ≠ 7

Given that the second equation is not satisfied, then (0, -2) is not a solution

(-9, -6)

7(-9) - 4(-6) = 8

-81 + 24 ≠ 8

-2(-9) + 3(-6) = 7

18 - 18 ≠ 7

Given that the equations are not satisfied, then (-9, -6) is not a solution

(7,7)

7(7) - 4(7) = 8

49 - 28 ≠ 8

-2(7) + 3(7) = 7

-14 + 21 = 7

Given that the first equation is not satisfied, then (7, 7) is not a solution