Question

In the accompanying diagram of circle O, COA is adiameter, O is the origin, OA = 1, and mLBOA = 30. Whatare the coordinates of B?

Answer 1

Given:

COA is a diameter

O is the origin

OA = 1

m< BOA = 30

Re-drawing the diagram to show the coordinates of the B:

Let the coordinates of B be (x,y)

Using trigonometric ratio, we can find the length of side AB

From trigonometric ratio, we have:

`tan\text{ }\theta\text{ = }(opposite)/(adjacent)`

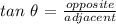
Substituting we have:

`\begin{gathered} tan\text{ 30 = }(y)/(1) \\ Cross-Multiply \\ y\text{ = tan30 }*\text{ 1} \\ y\text{ = 0.577} \\ y\text{ }\approx\text{ 0.58} \end{gathered}`

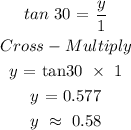
Hence, the coordinates of B is (1, 0.58)