Answer:
No solution
Explanation:
We have

For the sum it is not correct to assume
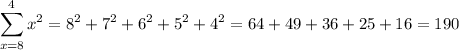
Note that for
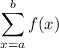
it is assumed
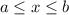 and in your case
and in your case
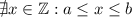 for
for

In fact, considering a set
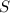 we have
we have
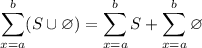 that satisfy
that satisfy
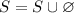
This means that, by definition

Therefore,

because the sum is empty.
For
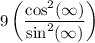
we have other problems. Actually, this case is really bad.
Note that
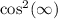 has no value. In fact, if we consider for the case
has no value. In fact, if we consider for the case
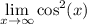 , the cosine function oscillates between
, the cosine function oscillates between
![[-1, 1]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/tg2u07b8rchn72pc0ki27b.png) , and therefore it is undefined. Thus, we cannot evaluate
, and therefore it is undefined. Thus, we cannot evaluate
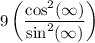
and then

has no solution