Question

A 244 kg motorcycle is travelling with aspeed of 14.7 m-s-1A) Calculate the kinetic energy (in J) of themotorcycle.B) If the speed of the motorcycle is increasedby a factor of 1.6, by what factor does itskinetic energy change?C) Calculate the speed (in m-s-1) of themotorcycle if its kinetic energy is 1/3 of thevaluefound in (a).

Answer 1

Given data:

* The mass of the motorcycle is m = 244 kg.

* The speed of the motorcycle is u = 14.7 m/s.

Solution:

(A). The kinetic energy of the motorcycle is,

`K_1=(1)/(2)mu^2`

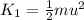
Substituting the known values,

`\begin{gathered} K_1=(1)/(2)*244*(14.7)^2_{} \\ K_1=26362.98\text{ J} \end{gathered}`

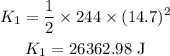
Thus, the value of kinetic energy is 26362.98 J.

(B). If the speed of the motorcycle is increased by a factor of 1.6,

`\begin{gathered} v=14.7*1.6 \\ v=23.52\text{ m/s} \end{gathered}`

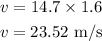
Thus, the kinetic energy of the motorcycle becomes,

`\begin{gathered} K_2=(1)/(2)mv^2 \\ K_2=(1)/(2)*244*(23.52)^2 \\ K_2=67489.23\text{ m/s} \end{gathered}`

Dividing K_2 by K_1,

`\begin{gathered} (K_2)/(K_1)=(67489.23)/(26362.98) \\ (K_2)/(K_1)=2.56 \end{gathered}`

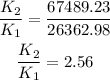
Thus, the kinetic energy is increased by the factor of 2.56.

(C). The 1/3 of the kinetic energy in the first part is,

`\begin{gathered} K=(1)/(3)* K_1 \\ K=(1)/(3)*26362.98 \\ K=8787.66\text{ J} \end{gathered}`

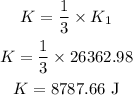
Thus, the speed of the motorcycle with the kinetic energy K is,

`\begin{gathered} K=(1)/(2)mv^2_{}_{} \\ 8787.66=(1)/(2)*244* v^2 \\ 8787.66=122* v^2 \end{gathered}`

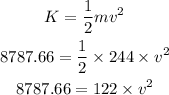
By simplifying,

`\begin{gathered} v^2=(8787.66)/(122) \\ v^2=72.03 \\ v\approx8.5\text{ m/s} \end{gathered}`

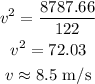
Thus, the speed of the motorcycle is 8.5 m/s.