Question

flying against the wind, an airplane travels 7840 kilometers in 8 hours. flying with the wind, the same plane travels 5280 kilometers in 4 hours. what is the rate of the plane in still air and what is the rate of the wind?

Answer 1

The rate of the plane in still air is 1150km/hr and the rate of the plane in the wind is 170km/hr.

Explanations:

The formula for calculating distance is expressed as:

`\begin{gathered} dis\tan ce=\text{speed}*\text{time} \\ d=st \end{gathered}`

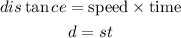
Let the rate of the plane in still air be "x"

Let the rate of the plane in the wind be "y"

if flying against the wind, an airplane travels 7840 kilometers in 8 hours, then;

8 (x - y) = 7840

x - y = 980 ........................ 1

If flying with the wind, the same plane travels 5280 kilometers in 4 hours

4 (x + y) = 5280

x + y = 1,320 ......................2

Add both equations:

x + x = 980 + 1320

2x = 2,300

x = 2300/2

x = 1150 km/hr

Substract x = 1150km/hr into equation 1.

x - y = 1320

1150 + y = 1320

y = 1320 - 1150

y = 170km/hr

Hence the rate of the plane in still air is 1150km/hr and the rate of the plane in the wind is 170km/hr