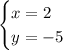For the information given in the statement you have
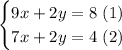
Using the elimination method, multiply by -1 the equation (2) and then add the equations to eliminate one of the variables
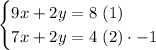

Now plug the value of x found into any of the initial equations to find the value of y. For example in equation (1)
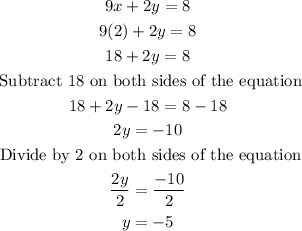
Therefore, the solutions of the system of equations are