The work required to stretch a string is given by the following equation:
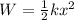
Where:
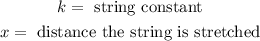
If the string is stretched 2 cm then we substitute the value of "x = 2" in the formula, we get:
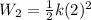
Solving the square and simplifying:
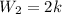
Now, if the string is stretched 1 cm we get:
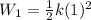
Solving the operations:
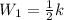
Now, we determine the quotient between W2 and W1:
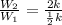
Simplifying we get:
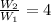
Now, we multiply both sides by W2:
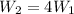
Therefore, the work required to stretch the string 2 cm is 4 times the work to stretch it 1 cm.