Question

Which of the following could be an example of a function with a domain (-0,) and a range (-0,2)? Check all that apply. A. V= - (0.25)* - 2 - B. v= -(3)*-2 O c. v= -(3)*+2 1 v= - (0.25)*+2 D.

Answer 1

It is desired that the domain and range of the function should, respectively, be

`\begin{gathered} \text{Domain}=(-\infty,\infty) \\ \text{Range}=(-\infty,2) \end{gathered}`

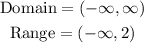
Observe the given choices of function.

It is evident that all the functions are exponential functions, so their domain must be the set of all real numbers,

`(-\infty,\infty)`

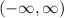
Now, we have to check the range of each of the 4 given functions.

Option A:

The function is given as,

`y=-(0.25)^x-2`

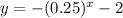
Consider the following,

`\begin{gathered} x\rightarrow\infty\Rightarrow-(0.25)^x\rightarrow0\Rightarrow-(0.25)^x-2\rightarrow-2\Rightarrow y\rightarrow-2 \\ x\rightarrow-\infty\Rightarrow-(0.25)^x\rightarrow-\infty\Rightarrow-(0.25)^x-2\rightarrow-\infty\Rightarrow y\rightarrow-\infty \end{gathered}`

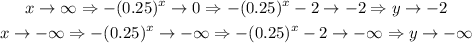
Thus, we see that the range of the function is,

`\text{Range}=(-\infty,-2)`

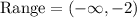
Since this does not match with the desired range. This is not a correct choice.

Option B:

The function is given as,

`y=-(3)^x-2`

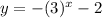
Consider the following,

`\begin{gathered} x\rightarrow\infty\Rightarrow-(3)^x\rightarrow-\infty\Rightarrow-(3)^x-2\rightarrow-\infty\Rightarrow y\rightarrow-\infty \\ x\rightarrow-\infty\Rightarrow-(3)^x\rightarrow0\Rightarrow-(3)^x-2\rightarrow-2\Rightarrow y\rightarrow-2 \end{gathered}`

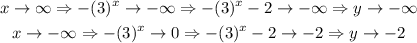
Thus, we see that the range of the function is,

`\text{Range}=(-\infty,-2)`

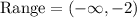
Since this does not match with the desired range. This is not a correct choice.

Option C:

The function is given as,

`y=-(3)^x+2`

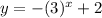
Consider the following,

`\begin{gathered} x\rightarrow\infty\Rightarrow-(3)^x\rightarrow-\infty\Rightarrow-(3)^x+2\rightarrow-\infty\Rightarrow y\rightarrow-\infty \\ x\rightarrow-\infty\Rightarrow-(3)^x\rightarrow0\Rightarrow-(3)^x+2\rightarrow2\Rightarrow y\rightarrow2 \end{gathered}`

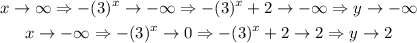
Thus, we see that the range of the function is,

`\text{Range}=(-\infty,2)`

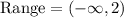
Since this exactly matches with the desired range. This is a correct choice.

Option D:

The function is given as,

`y=-(0.25)^x+2`

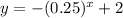
Consider the following,

`\begin{gathered} x\rightarrow\infty\Rightarrow-(0.25)^x\rightarrow0\Rightarrow-(0.25)^x+2\rightarrow2\Rightarrow y\rightarrow2 \\ x\rightarrow-\infty\Rightarrow-(0.25)^x\rightarrow-\infty\Rightarrow-(0.25)^x-2\rightarrow-\infty\Rightarrow y\rightarrow-\infty \end{gathered}`

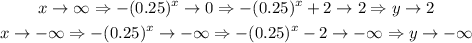
Thus, we see that the range of the function is,

`\text{Range}=(-\infty,2)`

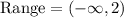
Since this exactly matches with the desired range. This is also a correct choice.

Thus, the we see that the functions in option C and D possess the desired domain and range.

Therefore, option C and option D are t