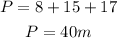The figure in the picture shows 3 squares that form a right triangle. Each side of the triangle is determined by one side of the squares.
The only information we know is the area of two of the squares. The area of a square is calculated as the square of one of its sides
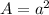
So to determine the side lengths of the squares, we can calculate the square root of the given areas:
![\begin{gathered} A=a^2 \\ a=\sqrt[]{A} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gchn6u3oqlgncm6b9k60j4wdir22qc0mum.png)
For one of the squares, the area is 64m², you can determine the side length as follows:
![\begin{gathered} a=\sqrt[]{64} \\ a=8 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zuer53g4jerxlkjdngdry8mw0zi33pox81.png)
For the square with an area 225m², the side length can be calculated as follows:
![\begin{gathered} a=\sqrt[]{225} \\ a=15 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rcgcl4shpsqwjgwliuwcgykdpwzbgudl2c.png)
Now, to determine the third side of the triangle, we have to apply the Pythagorean theorem. This theorem states that the square of the hypothenuse (c) of a right triangle is equal to the sum of the squares of its sides (a and b), it can be expressed as follows:

If we know two sides of the triangle, we can determine the length of the third one. In this case, the missing side is the hypothenuse (c), to calculate it you have to add the squares of the sides and then apply the square root:
![\begin{gathered} c^2=225+64 \\ c=\sqrt[]{225+64} \\ c=\sqrt[]{289} \\ c=17 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/k77l26inu86h3usnqpoguhs979uq0r75xn.png)
So the triangle's sides have the following lengths: 8, 15 and, 17
Now that we know the side lengths we can calculate the perimeter of the triangle. The perimeter of any shape is calculated by adding its sides: