Given the function:
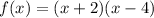
You can rewrite it as follows:
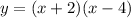
You need to remember that the y-value is zero when the function intersects the x-axis. Then, you need to make it equal to zero, in order to find the x-intercepts:
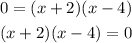
Solving for "x", you get these two values:
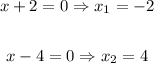
In order to find the vertex, you can follow these steps:
1. Find the x-coordinate of the vertex with this formula:
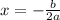
To find the value of "a" and "b", you need to multiply the binomials of the equation using the FOIL Method. This states that:
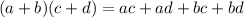
Then, in this case, you get:
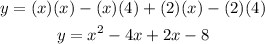
Add the like terms:
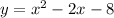
Notice that, in this case:
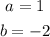
Then, you can substitute values into the formula and find the x-coordinate of the vertex of the parabola:
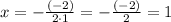
2. Substitute that value of "x" into the function and then evaluate, in order to find the y-coordinate of the vertex:
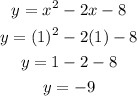
Therefore, the vertex of the parabola is:
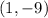
Knowing the x-intercepts and the vertex of the parabola, you can graph it.
Hence, the answer is: