Question

Find the lateral surface area and volume of the object in picture below

Answer 1

So first of all we have to find the lateral surface of the truncated pyramid. This surface is composed of 4 equal trapezoids. The are of a trapezoid is given by half the sum of its bases multiplied by its height. The large base of these faces are 6' long, the short base are 5' long and their height are 2.1' long. Then the area of each trapezoid is:

`((6^(\prime)+5^(\prime)))/(2)\cdot2.1^(\prime)=11.55in^2`

Then the total lateral surface is:

`11.55in^2\cdot4=46.2in^2`

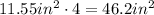
Then we need to find the volume of the truncated pyramid. This is given by the following formula:

`(1)/(3)h(a^2+ab+b^2)`

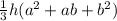
Where a and b are the bottom and top side of its two square faces and h is the height of the pyramid i.e. the vertical distance between bases. The lengths of the bases is 5' and 6' whereas the height of the pyramid is 2' then its volume is given by:

`(1)/(3)\cdot2^(\prime)\cdot(5^(\prime2)+6^(\prime)\cdot5^(\prime)+6^(\prime2))=60.7in^3`

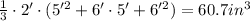
In summary, the lateral surface is 46.2in² and the volume is 60.7in³.