ANSWER
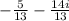
Step-by-step explanation
We want to divide the given complex fraction:
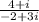
To do this, we have to rationalize the denominator of the fraction by multiplying the given fraction by another fraction made up of the conjugate of the denominator of the given fraction:
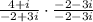
Simplifying this, we have:
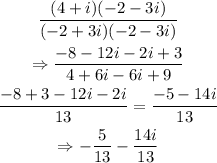
That is the solution of the division.