Question

Find the mean for the data set. 6, 14, 7, 4, 12, 8, 13, 4, 18, 14

Answer 1

Concept:

Mean is just another name for average. To find the mean of a data set, add all the values together and divide by the number of values in the set. The result is your mean!

The values are given below as

`6,14,7,4,12,8,13,4,18,14`

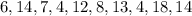
The image below shows how to calculate the mean

By substituting values, we will have

`\begin{gathered} \bar{x}=\frac{\sum ^{}_(n\mathop=0)x}{n} \\ n=10 \end{gathered}`
`\begin{gathered} \bar{x}=(6+14+7+4+12+8+13+4+18+14)/(10) \\ \bar{x}=(100)/(10) \\ \bar{x}=10 \end{gathered}`

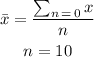
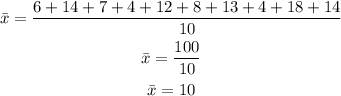
Hence,

The mean = 10

To calculate the variance, we will use the formula below

`^{}\sigma^2=\frac{\sum ^(\infty)_(n\mathop=0)(x-\bar{x})^2}{n}`

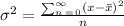
`\begin{gathered} \sigma^2=\frac{\sum ^(\infty)_{n\mathop{=}0}(x-\bar{x})^2}{n} \\ \sigma^2=(210)/(10) \\ \sigma^2=(210)/(10) \\ \sigma^2=21 \end{gathered}`

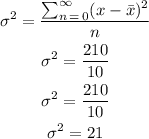
Hence

The variance = 21

To calculate the standard deviation,

`\begin{gathered} \sigma=\sqrt[]{variance} \\ \sigma=\sqrt[]{21} \\ \sigma=4.58 \end{gathered}`

Hence,

The standard deviation is = 4.58