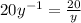Operation on rational expressions
Step 1: division of fractions
The division of two fractions is the same as multiplying the first by the inverted second fraction:
Then, in this case:
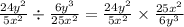
Step 2: multiplication of two fractions
We multiply two fractions by multiplying the numerators and the denominators:
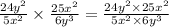
Step 3: simplifying the numbers of the fraction
We know that

Then, we can use this in our fraction:
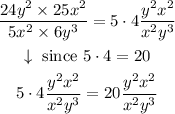
Step 4: exponents of the result
We know that if we have a division of same base expressions (same letters), the exponent is just a substraction:
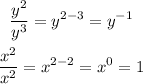
Then,
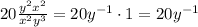
Since negative exponents correspond to a division, then we can express the answer in two different ways:
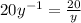
Answer: