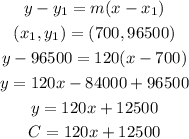Given:
Cost function is defined as,
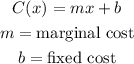
a) Fixed cost = $100, 50 items cost $1600.
The cost function is given as,

So, the cost function is,
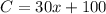
b) Fixed cost = $400, 10 items cost $650.
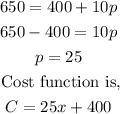
c) Fixed cost= $1000, 40 items cost $2000 .
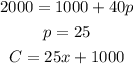
d) Fixed cost = $8500, 75 items cost $11,875.
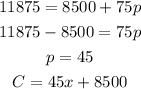
e) Marginal cost= $50, 80 items cost $4500.
In this case we know the value of m = 50 .
Use the slope point form,
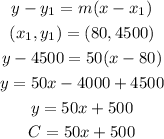
f) Marginal cost=$120, 100 items cost $15,800.
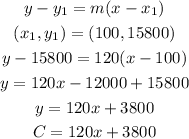
g) Marginal cost= $90,150 items cost $16,000.
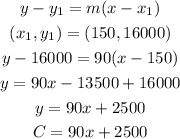
h) Marginal cost = $120, 700 items cost $96,500