Question

If a,b ,and c represent the set of all values of x that satisly the equation below, what is the value(A+ b+ c) + (abc)?X^3-20x = x^2(A) -1(B) 0(C) 1(D) 9

Answer 1

First, we need to find the solutions a, b, and c of the equation:

`x^3-20x=x^2`

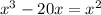
We can rewrite it as:

`\begin{gathered} x^3-x^(2)-20x=0 \\ \\ x(x^(2)-x-20)=0 \\ \\ x=0\text{ or }x^(2)-x-20=0 \end{gathered}`

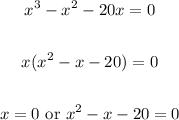
Thus, one of the solutions is a = 0.

To find the other solutions, we can use the quadratic formula. We obtain:

`\begin{gathered} x=\frac{-(-1)\pm\sqrt[]{(-1)^(2)-4(1)(-20)}}{2(1)} \\ \\ x=\frac{1\pm\sqrt[]{1+80}}{2} \\ \\ x=\frac{1\pm\sqrt[]{81}}{2} \\ \\ x=(1\pm9)/(2) \\ \\ b=(1-9)/(2)=-4 \\ \\ c=(1+9)/(2)=5 \end{gathered}`

Now, we need to find the value of the expression:

`\mleft(a+b+c\mright)+abc`

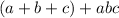
Using the previous solutions, we obtain:

`\mleft(0-4+5\mright)+0(-4)(5)=1+0=1`

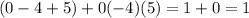
Therefore, the answer is 1.