Question

Write a quadratic equationwith vertex (3,-6) and otherpoint (-7,14). Solve for a!

Answer 1

We have to find the parameter a of a quadratic equation knowing the following

• The vertex is (3,-6).

,

• A random point is (-7,14).

Based on the given information, we have the following

`\begin{gathered} h=3 \\ k=-6 \\ x=-7 \\ y=14 \end{gathered}`

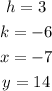
The vertex form of a quadratic equation is

`y=a(x-h)^2+k`

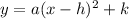
Replacing all the givens, we have

`14=a(-7-3)^2-6`

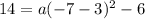
Now, we solve for a

`\begin{gathered} 14=a(-10)^2-6 \\ 14=a(100)-6 \\ 14+6=100a \\ 100a=20 \\ a=(20)/(100)=(1)/(5) \end{gathered}`

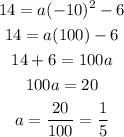
Therefore, a is equal to 1/5.