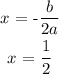Question

Consider the quadratic f(x)=x^2-x-30Determine the following ( enter all numerical answers as integers,fraction or decimals$The smallest (leftmost) x-intercepts is x=The largest (rightmost)x-intercepts is x=The y-intercept is y=The vertex is The line of symmetry has the equation

Answer 1

Smallest x-intercept: x = -5

Largest x-intercept: x = 6

y-intercept: y = -30

The vertex is (1/2, -121/4)

Line of symmetry x = 1/2

Step-by-step explanation

Given:

`f(x)\text{ = x}^2\text{ - x - 30}`

Desired Results:

1. Smallest x-intercept: x =

2. Largest x-intercept: x =

3. y-intercept: y =

4. The vertex is

5. Equation of Line of symmetry

1. Determine the x-intercepts by equating f(x) to zero (0).

`\begin{gathered} 0\text{ = x}^2-x-30 \\ x^2-6x+5x-30\text{ = 0} \\ x(x-6)+5(x-6)=0 \\ (x-6)(x+5)=0 \\ x-6=0,\text{ x+5=0} \\ x\text{ = 6, x = -5} \end{gathered}`

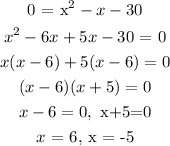
The smallest and largest x-intercepts are -5 and 6 respectively.

2. Determine the y-intercept by equating x to 0

`\begin{gathered} y\text{ = \lparen0\rparen}^2-0-30 \\ y\text{ = -30} \end{gathered}`

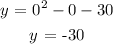
y-intercept is -30

3a. Determine the x-coordinate of the vertex using the formula

`x\text{ = -}(b)/(2a)`

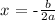
where:

a = 1

b = -1

Substitute the values

`\begin{gathered} x\text{ = -}((-1))/(2(1)) \\ x\text{ = }(1)/(2) \end{gathered}`

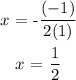
3b. Determine the y-coordinate of the vertex by substituting x into the equation

`\begin{gathered} y\text{ = \lparen}(1)/(2))^2-(1)/(2)-30 \\ y\text{ = }(1)/(4)-(1)/(2)-30 \\ Find\text{ LCM} \\ y\text{ = }(1-2-120)/(4) \\ y\text{ = -}(121)/(4) \end{gathered}`

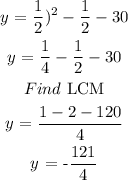
4. Determine the line of symmetry

In standard form the line of symmetry of a quadratic function can be identified using the formula

`\begin{gathered} x\text{ = -}(b)/(2a) \\ x\text{ = }(1)/(2) \end{gathered}`