Question

A person invested $3,700 in an account growing at a rate allowing the money to double every 6 years. How much money would be in the account after 14 years, to the nearest dollar?

Answer 1

Given :

The principal = 3,700

Assume a simple interest

The account growing at a rate allowing the money to double every 6 years.

So,

`\begin{gathered} I=P\cdot r\cdot t \\ I=P \\ 3700=3700\cdot r\cdot6 \\ r=(1)/(6) \end{gathered}`

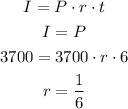
How much money would be in the account after 14 years, to the nearest dollar?​

So, we will substitute with r = 1/6, t = 14 years

So,

`\begin{gathered} I=3700\cdot(1)/(6)\cdot14=8633.33 \\ \\ A=P+I=8633.33+3700=12333.33 \end{gathered}`

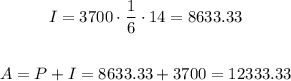
Rounding to the nearest dollar

So, the answer will be $12,333