Given:
The mass of the child and the sled is,
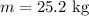
The child acquires a speed at the bottom of the hill is,
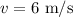
To find:
The height of the hill
Step-by-step explanation:
The potential energy at the top of the hill will be converted to the potential energy at the bottom of the hill. So for the hill of height 'h', we can write, the potential energy as
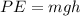
The kinetic energy is
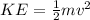
So,
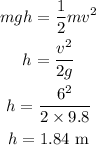
Hence, the height of the hill is 1.84 m.