Question

Khalid is investigating two linear functions. The first linear function is defined by the equation 2x + 3y = 12. The second linear functionpasses through the points (3,-2) and (-2, k).For the case where the two linear functions have the same y-intercept, what must be the value of k?k=

Answer 1

According to the given data we have the following:

first linear function is defined by the equation 2x + 3y = 12

second linear function passes through the points (3,-2) and (-2, k)

the two linear functions have the same y-intercept

k?

To calculate k first we have to do the following:

we would have to use the formula y=mx +b

the two linear functions have the same y-intercept, therefore, b=12.

So, y=mx +12

As second linear function passes through the points (3,-2) we are going to substitue the x and y with 3 and -2.

So, -2=m*3+12

-2-12=m*3

-14=m*3

m=-14/3

m=-4

Finally we would calculate k by writiing the equation of the line that passes through each pair of points as follows:

y2-y1/x2-x1=m

So

`\frac{k\text{ -(-2)}}{\text{-2 - 3}}\text{ }=\text{ -4}`

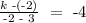
So, k +2/-5=-4

k+2=20

k=20-2

k=18