The final answer is: 27%
We are asked to find the probability that a student chosen at random is a junior. This requires that we know the total number of students in each level from Freshmen to Seniors.
Totals:
Freshmen = 4 + 3 = 7
Sophomore = 6 + 4 = 10
Juniors = 2 + 6 = 8
Seniors = 2 + 3 = 5
Thus we can calculate the total number of students considered:
7 + 10 + 8 + 5 = 30 students in total.
Now we can calculate the probability as:
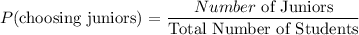
The number of Juniors was calculated earlier as: Juniors = 8
We have the total number of students as 30
Therefore, we can solve:
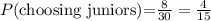
But we were asked to round to the nearest whole percent, which means we are required to put the fraction into percentage.
The way we do this is to multiply the fraction by 100%
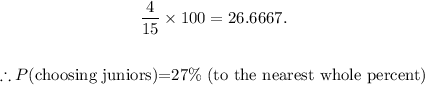
Therefore the final answer is: 27%