Question

Find a.Round to the nearest tenth:a10 cm150°12°с=a = [ ? ]cmLaw of Sines: sin A=sin Bbasin cСEnter

Answer 1

24.0 cm

Step-by-step explanation:

To find the value of a, we will use the Law of sines, so

`(\sin A)/(a)=(\sin B)/(b)`

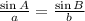
So, replacing A = 150°, B = 12°, and b = 10 cm, we get:

`(\sin150)/(a)=(\sin 12)/(10)`

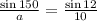
Now, we need to solve for a. First, cross multiply

`10\cdot\sin 150=a\cdot\sin 12`

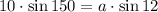
Then, divide by sin12

`\begin{gathered} (10\cdot\sin150)/(\sin12)=(a\cdot\sin 12)/(\sin 12) \\ (10\cdot(0.5))/(0.208)=a \\ 24.0=a \end{gathered}`

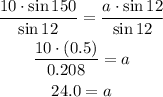
Therefore, a = 24.0 cm