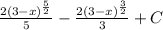Question

Evaluate the indefinite integral using substitution method.


`\displaystyle \large{\int {(x-2)√(3-x)} \ dx }`

Answer 1

`\frac{2(3 - x)^{ (5)/(2) } }{5} - \frac{2(3 - x)^{ (3)/(2) } }{3} + C`is the answer

Explanation:-

Given:

`{\int {(x-2)√(3-x)} \ dx }`

Differentiate on both sides,

`{\int {(x-2)√(3-x)} \ dx },u = 3 - x`

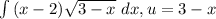
Isolate and substitute back,

`{\int {(x-2)√(3-x)} \ * ( - 1) du },u = 3 - x`

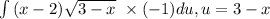
Substitute back,

`{\int ( - ( - u + 3 - 2) √(u))du }`

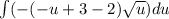
Applying property of integral ∫ kf(x)dx = k ∫ f(x)dxdx,

`- ∫ ( - u + 3 - 2) √(u) \: du,u = 3 - x`

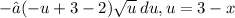
Combining like terms,

`- ∫ ( - u +1) √(u) \: du,u = 3 - x`

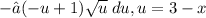
Now applying distributive property,

`- ∫ (( - u +1) √(u)) \: du,u = 3 - x`

`= > - ∫ ( - √(u) * u + √(u) )\: du,u = 3 - x`

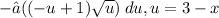
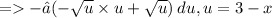
Converting to exponential form,

`- ∫ ( - u^{ (1)/(2) } * u + u^{ (1)/(2) } )\: du,u = 3 - x`

Multiplying the first two monomuals after integral, we get,

`- ∫ ( - u^{ (3)/(2) } + u^{ (1)/(2) } )\: du,u = 3 - x`

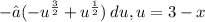
Now applying the prperty of ∫ f(x) + g(x)dx = ∫ f(x)dx + ∫ g(x)dx,

`- ( - ∫u^{ (3)/(2) } \: du + ∫u^{ (1)/(2) } \: du),u = 3 - x`

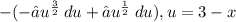
Now integrate the power rule,

`- ( - \frac{u^{ (5)/(2) }}{ (5)/(2) } + \frac{u^{ (3)/(2) }}{ (3)/(2) } ),u = 3 - x`

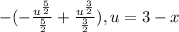
Divide the fractions by multiplying its reciprocals,

`- ( - u^{ (5)/(2) } * (2)/(5) + u^{ (3)/(2) } * (2)/(3)),u = 3 - x`

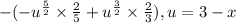
Now write as single fractions,

`- ( - \frac{2u^{ (5)/(2) } }{5} + \frac{2u^{ (3)/(2) } }{3})`

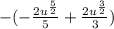
Removing the parentheses,

`\frac{2u^{ (5)/(2) } }{5} - \frac{2u^{ (3)/(2) } }{3},u = 3 - x`

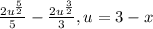
Substitute back,

`\frac{2(3 - x)^{ (5)/(2) } }{5} - \frac{2(3 - x)^{ (3)/(2) } }{3}`

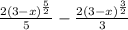
Now adding the constant of integration C∈R,

`\frac{2(3 - x)^{ (5)/(2) } }{5} - \frac{2(3 - x)^{ (3)/(2) } }{3} + C`

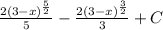
Hence, the answer.