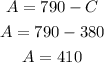Question

Josie sold 790 tickets to a local car show for a total of $4,390.00. A ticket for a Child costs $4.00 and adult ticket costs $7.00. How many of each ticket did she sell? A) Children’s ticket? B) Adult Ticket?

Answer 1

Let's define the following variables first.

A = number of tickets sold for adults

C = number of tickets sold for children

From the question, we can say that or form the following equations:

1. A + C = 790 tickets

2. $7A + $4C = $4, 390

The first equation can also be written as A = 790 - C. We can use this equation and replace "A" in the second equation.

`7(790-C)+4c=4,390`

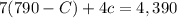
From that, we can solve "C" by solving the equation formed above.

`\begin{gathered} \text{Distribute 7 to the terms inside the parenthesis.} \\ 7(790)-7(C)+4C=4,390 \\ 5,530-7C+4C=4,390 \\ \text{Subtract 5,530 on both sides of the equation.} \\ -7C+4C=-1140 \\ -3C=-1140 \\ \text{Divide -3 on both sides.} \\ C=380 \end{gathered}`

Therefore, 380 tickets for children were sold.

Since there are 790 tickets in total that are sold and 380 tickets for children were sold, we can say that 410 tickets for adult was sold.

`\begin{gathered} A=790-C \\ A=790-380 \\ A=410 \end{gathered}`