Question

Find the (x , y) coordinate(s) of any hole(s) in h( x ). If there is none, write “n/a”.Round to two decimals.

Answer 1

The hole appears in the rational function when the numerator and the denominator have the same zeroes

Since the rational function is

`h(x)=(x+7)/(x^2-49)`

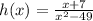
Factorize the denominator

`x^2-49=(x+7)(x-7)`

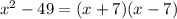
The rational function h(x) is

`h(x)=(x+7)/((x+7)(x-7))`

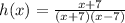
Since (x + 7) is in both numerator and denominator

Then there is a hole at x + 7 = 0

Let us find the value of x

`\begin{gathered} x+7=0 \\ x+7-7=0-7 \\ x=-7 \end{gathered}`

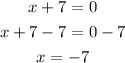
The whole is at x = -7

Then simplify the fraction to find the value of y at x = -7

`h(x)=((x+7))/((x+7)(x-7))`

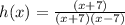
Cancel the bracket (x+7) up by the same bracket down

`h(x)=(1)/(x-7)`

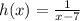
Substitute x by -7

`\begin{gathered} h(-7)=(1)/(-7-7) \\ h(-7)=(1)/(-14) \\ y=-(1)/(14) \end{gathered}`

The hole is at (-7, -1/14)