Answer:
Perpendicular
Explanation:
B. Their slopes (or gradients). To determine whether two lines on a plane are parallel or perpendicular, we need to examine what their slopes are. You can do this by using:
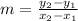 .
.
So for the first line, it'll be:
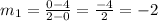
And for the second line, it'll be:
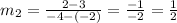
If two lines are parallel, their slopes will be the same. If two lines are perpendicular, one line's slope will be the negative reciprocal of the other; this means you can express the relationship between the two slopes
 and
and
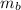 as
as
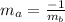 .
.
So we can see immediately the two lines aren't parallel, since the two slopes are different (one is -2 and the other is 1/2). However, they are perpendicular since if we do
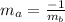 where
where
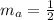 and
and
 , we see that the equation is true (
, we see that the equation is true (
 ).
).