Answer:
1.22 m/s² (3 s.f.)
Step-by-step explanation:
Draw a diagram modelling the given situation (see attachment).
- F = Friction.
Friction always acts in the opposite direction to motion (or potential motion). - R = Normal Reaction (perpendicular to the plane).
- Weight = mg.
Given values:
- Pulling force = 84.4 N
- Mass (m) = 14 kg
- Acceleration due to gravity (g) = 9.8 m/s²
- Coefficient of friction (μ) = 0.3
As the pulling force is at an angle to the plane (ground), resolve the force into components parallel and perpendicular to the plane.
Resolving vertically (↑) to find the Normal Reaction, R:
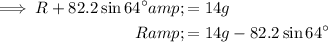
The frictional force takes its maximum value when an object starts to move (or is on the point of moving):
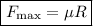
where R is the Normal Reaction and μ is the coefficient of friction.
Using F = μR to find the Frictional Force, F:

Newton's second law states that the overall resultant force acting on a body is equal to the mass of the body multiplied by the body’s acceleration:
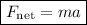
Resolving horizontally (→) using Newton's second law of motion to find acceleration:

Therefore, the acceleration of the box is 1.22 m/s² (3 s.f.).