Question

Prove the following


`\sf \cos \bigg( (3\pi)/(2) + x \bigg) \cos \: (2\pi + x) \bigg \{ \cot \bigg( (3\pi)/(2) - x \bigg) + cot(2\pi + x) \bigg \} = 1`

- Required step by step explanation
- Spam will be reported on spot.​

​

Answer 1

Explanation:

Hence,

`\boxed{\tt{ \cos \bigg( (3\pi)/(2) + x \bigg) \cos \: (2\pi + x) \bigg \{ \cot \bigg( (3\pi)/(2) - x \bigg) + cot(2\pi + x) \bigg \} = 1}}`

▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬

Answer 2

Explanation:

`\large\underline{\sf{Solution-}}`

Consider

`\rm \: \cos \bigg( (3\pi)/(2) + x \bigg) \cos \: (2\pi + x) \bigg \{ \cot \bigg( (3\pi)/(2) - x \bigg) + cot(2\pi + x) \bigg \}cos(23π+x)cos(2π+x)`

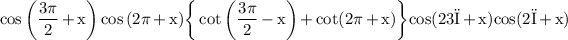
We Know,

`\rm \: \cos \bigg( (3\pi)/(2) + x \bigg) = sinx`

`\rm \: {cos \: (2\pi + x) }`

`\rm \: \cot \bigg( (3\pi)/(2) - x \bigg) \: = \: tanx`

`\rm \: cot(2\pi + x) \: = \: cotx`

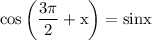
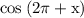
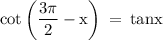
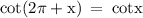
So, on substituting all these values, we get

`\rm \: = \: sinx \: cosx \: (tanx \: + \: cotx)`

`\rm \: = \: sinx \: cosx \: \bigg((sinx)/(cosx) + (cosx)/(sinx)`

`\rm \: = \: sinx \: cosx \: \bigg(\frac{ {sin}^(2)x + {cos}^(2)x}{cosx \: sinx}`

`\rm \: = \: 1=1`

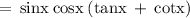
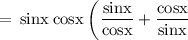
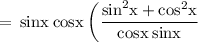
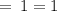
Hence,

`\boxed{\tt{ \cos \bigg( (3\pi)/(2) + x \bigg) \cos \: (2\pi + x) \bigg \{ \cot \bigg( (3\pi)/(2) - x \bigg) + cot(2\pi + x) \bigg \} = 1}}`

▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬

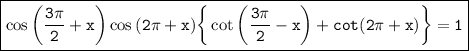
ADDITIONAL INFORMATION :-

Sign of Trigonometric ratios in Quadrants

• sin (90°-θ) = cos θ
• cos (90°-θ) = sin θ
• tan (90°-θ) = cot θ
• csc (90°-θ) = sec θ
• sec (90°-θ) = csc θ
• cot (90°-θ) = tan θ
• sin (90°+θ) = cos θ
• cos (90°+θ) = -sin θ
• tan (90°+θ) = -cot θ
• csc (90°+θ) = sec θ
• sec (90°+θ) = -csc θ
• cot (90°+θ) = -tan θ
• sin (180°-θ) = sin θ
• cos (180°-θ) = -cos θ
• tan (180°-θ) = -tan θ
• csc (180°-θ) = csc θ
• sec (180°-θ) = -sec θ
• cot (180°-θ) = -cot θ
• sin (180°+θ) = -sin θ
• cos (180°+θ) = -cos θ
• tan (180°+θ) = tan θ
• csc (180°+θ) = -csc θ
• sec (180°+θ) = -sec θ
• cot (180°+θ) = cot θ
• sin (270°-θ) = -cos θ
• cos (270°-θ) = -sin θ
• tan (270°-θ) = cot θ
• csc (270°-θ) = -sec θ
• sec (270°-θ) = -csc θ
• cot (270°-θ) = tan θ
• sin (270°+θ) = -cos θ
• cos (270°+θ) = sin θ
• tan (270°+θ) = -cot θ
• csc (270°+θ) = -sec θ
• sec (270°+θ) = cos θ
• cot (270°+θ) = -tan θ