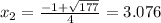Hello, in this question we will use the "Sinus Theorem".
The general formula of the Sine Theorem is as follows;
We are given the length of the two sides and the sine value of the angle of the unknown side. We also know the area of the triangle. Let's substitute the required values in this formula to get the result.
In the last step, we are left with a quadratic equation with one unknown. To solve this equation, we need to calculate the discriminant value.
There are only two roots of a quadratic equation with one unknown.
Thus our x values;
We cannot accept the first root
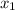 . Because length cannot be a negative value.
. Because length cannot be a negative value.
Ans =