Question

I need help on this question

Answer 1

Real zeros are: x = 0, x = 1 and x =2

***Your graph is incorrect. See mine for the correct graph***

Explanation:

We have the polynomial

`$\displaystyle \:x^(4)-3x^(3)+2x^(2)\:=\:0$`

`\mathrm{Factor\:out\:common\:term\:}x^2:\\\\`

`=x^2\left(x^2-3x+2\right)`

`\mathrm{Factor}\:x^2-3x+2:`

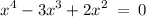
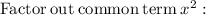
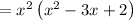
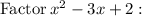
For an expression of the form ax² + bx + c we can find factors if we find two values u and v such uv = c and u + v =b and factor into (ax +ux)+ (vx+c)

We have here a = 1, b = -3 c = 2

==> u = -1, v = -2

`\:x^2-3x+2 = (x-1)(x-2)`

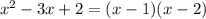
So the original expression becomes

`\:x^2-3x+2 = x^2\left(x-1\right)\left(x-2\right)`

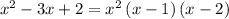
To find the zeros, set this equal to 0 and solve for x

`x^2\left(x-1\right)\left(x-2\right)=0`

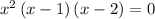
We end up with 3 roots corresponding to the 0 values for each of the three terms

`x^2 = 0 == > x = \pm 0 = 0\\\\`

`(x - 1) = 0 == > x = 1\\\\(x - 2) = 0 == > x = 2\\\`

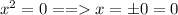
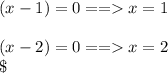
Answer real zeros are: x = 0, x = 1 and x =2

**** Your graph is incorrect. Check mine. The zeros happen where the curve intersects the x axis and these are at x = 0, x = 1, x =2