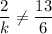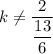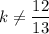Question

Consider the system of equations:

-2x + Ky = 26
13x - 6у = -7
Find all values of k for which the system has exactly one solution. Choose "does not exist" if such a k does not exist.

Answer 1

Explanation:

First of all, if the system of equations has exactly one solution, then the graph of these two equations will intersect at exactly one point, which means their slopes will be different. If the slopes are the same, there could be infinitely many solutions or no solution.

Rearrange the first equation to solve for slope of
`-2x+ky=26`

y = (2/k)x + 26/k

The slope is 2/k.

The slope of the second equation is 13/6

as long as 2/k does not equal to 13/6, we have exactly one solution.

SO, the last step:

`(2)/(k) \\eq (13)/(6)\\`

`k \\eq (2)/((13)/(6))`

`k\\eq (12)/(13)`