Question

Solve for x and y 60° 15°

Answer 1

y = 4x hope this Helps!

Explanation:

y = kx

k = y/x = 60/15 = 4

y = 4x

Answer 2

The value of x = 7.5 units

The value of y= 12.99 units

The image shows a right triangle with a 60° angle, indicating that this is a 30°-60°-90° special right triangle. In such triangles, the sides are in a consistent ratio: the length of the side opposite the 30° angle is half that of the hypotenuse, and the length of the side opposite the 60° angle is
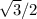`\( √(3)/2 \)` times the length of the hypotenuse.

Given that the hypotenuse (the side opposite the 90° angle) is 15, we can find x (the side opposite the 30° angle) and y (the side opposite the 60° angle) using the following steps:

1. Find x : Since x is opposite the 30° angle,
`\( x = (1)/(2) * \text{hypotenuse} \).`

2. Find y : Since y is opposite the 60° angle,
`\( y = (√(3))/(2) * \text{hypotenuse} \).`

Now we'll calculate these values.

In the 30°-60°-90° triangle given, the lengths of sides x and y are:

- x (opposite the 30° angle) is
`\( (1)/(2) * 15 = 7.5 \) units.`

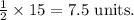
- y (opposite the 60° angle) is
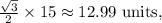`\( (√(3))/(2) * 15 \approx 12.99 \) units,` when rounded to two decimal places.