Question

Sketch the parabola using the given information. Vertex (0,-2), point (5,8)

Answer 1

Take into account that in a general way, a parabola can be written as follow:

y = a(x - h)^2 + k

where,

a: is the leadding coefficient

(h,k): vertex of the parabola

In order to graph the parabola, first calculate the value of a, by using the following information:

(h,k) = (0,-2)

(x,y) = (5,8)

Replace the previous values into the equation of the parabola and solve for a:

`\begin{gathered} 8=a(5-0)^2-2 \\ 8=25a-2 \\ a=(8+2)/(25)=(10)/(25)=(2)/(5) \end{gathered}`

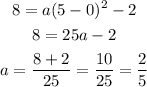
Then, the equation of the given parabola is:

`\begin{gathered} y=(2)/(5)(x-0)^2-2 \\ y=(2)/(5)x^2-2 \end{gathered}`

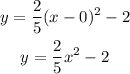
Another point could be:

x = -2

`\begin{gathered} y=(2)/(5)(-2)^2-2 \\ y=(2)/(5)(4)-2 \\ y=(8)/(5)-2 \\ y=-(2)/(5) \end{gathered}`

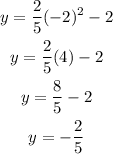
the point is (-2,-2/5).

Then, the graph is: