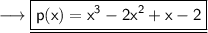Question

Find a polynomial function of degree 3 with 2, i, -i as zeros.

Answer 1

`p(x)= x^3-2x^2+x-2`

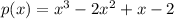
Explanation:

Here we are given that a polynomial has zeros as 2 , i and -i . We need to find out the cubic polynomial . In general we know that if
`\alpha , \ \beta \ \& \ \gamma` are the zeros of the cubic polynomial , then ,

`\sf \longrightarrow p(x)= (x -\alpha )(x-\beta)(x-\gamma)`

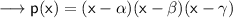
Here in place of the Greek letters , substitute 2,i and -i , we get ,

`\sf\longrightarrow p(x)= (x -2 )(x-i)(x+i)`

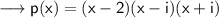
Now multiply (x-i) and (x+i ) using the identity (a+b)(a-b)=a² - b² , we have ,

`\sf \longrightarrow p(x)= (x-2)\{ x^2 - (i)^2\}`

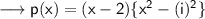
Simplify using i = √-1 ,

`\sf \longrightarrow p(x)= (x-2)( x^2 + 1 )`

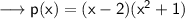
Multiply by distribution ,

`\sf \longrightarrow p(x)= x(x^2+1) -2(x^2+1)`

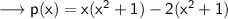
Simplify by opening the brackets ,

`\sf\longrightarrow p(x)= x^3+x-2x^2-2`

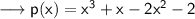
Rearrange ,

`\sf\longrightarrow \underline{\boxed{\blue{\sf p(x)= x^3-2x^2+x-2}}}`