Question

The domain and range of the graph above

Answer 1

Answers:

• Domain:
  `\boldsymbol{(-\infty, \infty)}`
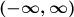
• Range:
  `\boldsymbol{[3,\infty)}`

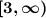
Note that there's a square bracket for the '3', but everything else is a curved parenthesis.

==================================================

Step-by-step explanation:

The domain is the set of all allowed x inputs. The arrows tell us that the parabola stretches forever in both left and right directions. We can plug in any x value we want, which means the domain is the set of all real numbers which means the interval notation for that is
`(-\infty, \infty)`

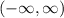
This is the same as writing the compound inequality
`-\infty < x < \infty`

--------------

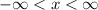
The range is the set of all possible y values. The lowest output is y = 3, which is where the vertex is located. We can have this output or anything larger.

So y = 3 or larger, which we can write
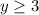`y \ge 3` and that flips to
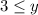`3 \le y` and further expands into
`3 \le y < \infty`

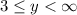
The interval notation for the range is therefore
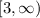`[3 ,\infty)`. We use a square bracket to include 3 as part of the range.