Question

Pleaseeeee ı dont find the answer

Answer 1

Answer:
`y(x) = \sqrt{(7x^(14))/(-2x^7+9)}\\\\`

==========================================================

Step-by-step explanation:

The given differential equation (DE) is

`y'-(7)/(x)y = (y^3)/(x^8)\\\\`

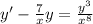
Which is the same as

`y'-(7)/(x)y = (1)/(x^8)y^3\\\\`

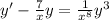
This 2nd DE is in the form
`y' + P(x)y = Q(x)y^n`

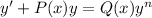
where

`P(x) = -(7)/(x)\\\\Q(x) = (1)/(x^8)\\\\n = 3`

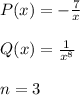
As the instructions state, we'll use the substitution
`u = y^(1-n)`

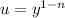
We specifically use
`u = y^(1-n) = y^(1-3) = y^(-2)`

-----------------

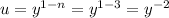
After making the substitution, we'll end up with this form

`(du)/(dx) + (1-n)P(x)u = (1-n)Q(x)\\\\`

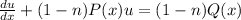
Plugging in the items mentioned, we get:

`(du)/(dx) + (1-n)P(x)u = (1-n)Q(x)\\\\(du)/(dx) + (1-3)*(-7)/(x)u = (1-3)(1)/(x^8)\\\\(du)/(dx) + (14)/(x)u = -(2)/(x^8)\\\\`

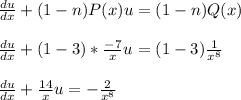
We can see that we have a new P(x) and Q(x)

`P(x) = (14)/(x)\\\\Q(x) = -(2)/(x^8)`

-------------------

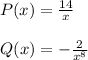
To solve the linear DE
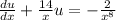`(du)/(dx) + (14)/(x)u = -(2)/(x^8)\\\\`, we'll need the integrating factor which I'll call m

`m(x) = e^(\int P(x) dx) = e^{\int (14)/(x)dx} = e^(14\ln(x))`

`m(x) = e^{\ln(x^(14))} = x^(14)`

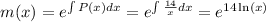
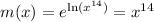
We will multiply both sides of the linear DE by this m(x) integrating factor to help with further integration down the road.

`(du)/(dx) + (14)/(x)u = -(2)/(x^8)\\\\m(x)*\left((du)/(dx) + (14)/(x)u\right) = m(x)*\left(-(2)/(x^8)\right)\\\\x^(14)*(du)/(dx) + x^(14)*(14)/(x)u = x^(14)*\left(-(2)/(x^8)\right)\\\\x^(14)*(du)/(dx) + 14x^(13)*u = -2x^6\\\\\left(x^(14)*u\right)' = -2x^6\\\\`

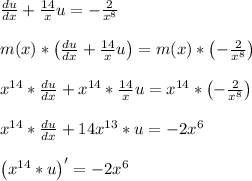
It might help to think of the product rule being done in reverse.

Now we can integrate both sides to solve for u

`\left(x^(14)*u\right)' = -2x^6\\\\\displaystyle \int\left(x^(14)*u\right)'dx = \int -2x^6 dx\\\\\displaystyle x^(14)*u = (-2x^7)/(7)+C\\\\\displaystyle u = x^(-14)*\left((-2x^7)/(7)+C\right)\\\\\displaystyle u = x^(-14)*(-2x^7)/(7)+Cx^(-14)\\\\\displaystyle u = (-2x^(-7))/(7)+Cx^(-14)\\\\`

`u = (-2)/(7x^7) + (C)/(x^(14))\\\\u = (-2)/(7x^7)*(x^7)/(x^7) + (C)/(x^(14))*(7)/(7)\\\\u = (-2x^7)/(7x^(14)) + (7C)/(7x^(14))\\\\u = (-2x^7+7C)/(7x^(14))\\\\`

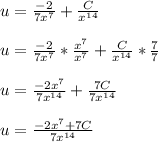
Unfortunately, this isn't the last step. We still need to find y.

Recall that we found
`u = y^(-2)\\\\`

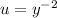
So,

`u = (-2x^7+7C)/(7x^(14))\\\\y^(-2) = (-2x^7+7C)/(7x^(14))\\\\y^(2) = (7x^(14))/(-2x^7+7C)`

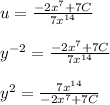
We're told that y(1) = 1. This means plugging x = 1 leads to the output y = 1. So the RHS of the last equation should lead to 1. We'll plug x = 1 into that RHS, set the result equal to 1 and solve for C

`(7*1^(14))/(-2*1^7+7C) = 1\\\\(7)/(-2+7C) = 1\\\\7 = -2+7C\\\\7+2 = 7C\\\\7C = 9\\\\C = (9)/(7)`

So,

`y^(2) = (7x^(14))/(-2x^7+7C)\\\\y^(2) = (7x^(14))/(-2x^7+7*(9)/(7))\\\\y^(2) = (7x^(14))/(-2x^7+9)\\\\y = \sqrt{(7x^(14))/(-2x^7+9)}\\\\`

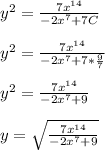
We go with the positive version of the root because y(1) is positive, which must mean y(x) is positive for all x in the domain.