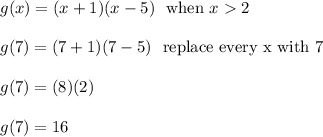Answer: 16
======================================================
Step-by-step explanation:
This is a piecewise function. As the name implies, the g(x) is broken up into 3 pieces. Each piece depends on what the input x is.
If x is between
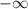 and
and
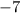 , excluding both endpoints, then we pick the first piece. So in this case,
, excluding both endpoints, then we pick the first piece. So in this case,
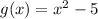
Or if
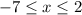 , then we go for the second piece and
, then we go for the second piece and
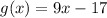
Lastly, if x is between
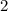 and
and
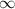 , then we go for the last piece and say
, then we go for the last piece and say

------------------
To paraphrase that last section, we have g(x) defined as having a split personality or multiple identities depending on what x is.
- If x is between negative infinity and -7 (exclusive), then g(x) = x^2-5
- If x is between -7 and 2, then g(x) = 9x-17
- If x is between 2 and infinity, then g(x) = (x+1)(x-5)
------------------
The question is: which piece do we pick?
Well, g(7) means that x = 7 for g(x). We'll pick the third piece because 7 is between 2 and infinity. In other words, x = 7 makes
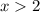 a true inequality.
a true inequality.
So,