Question

asked Mar 24, 2023 108k views

1 Answer

Rickie · Answer 1 · 2023-03-30T10:50:05+0000

Answer:

$\textsf{Let $\boxed{x}=\boxed{\textsf{The total dollar amount of all phone sales}}$}\:.$

$\textsf{Let $\boxed{y}=\boxed{\textsf{The total dollar amount of all computer sales}}$}\:.$

System of Equations

$\boxed{x + y = 3600}$

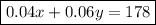
$\boxed{0.04x + 0.06y = 178}$

Explanation:

Given information:

Define the variables:

Convert the percentages into decimal form:

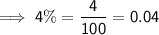
$\implies \sf 4\%=(4)/(100)=0.04$

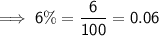
$\implies \sf 6\%=(6)/(100)=0.06$

Therefore, the system of equations that could be used to determine the dollar amount of phone sales and computer sales is:

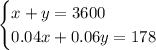
$\begin{cases}x + y = 3600\\0.04x + 0.06y = 178\end{cases}$

Solving the system of equations

Rewrite the first equation to isolate y:

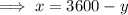
$\implies x=3600-y$

Substitute the expression for x into the second equation and solve for y:

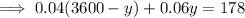
$\implies 0.04(3600-y)+0.06y=178$

$\implies 144-0.04y+0.06y=178$

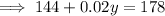
$\implies 144+0.02y=178$

$\implies 0.02y=34$

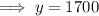
$\implies y=1700$

Therefore, Cameron made $1,700 of computer sales.

Substitute the found value of y into the first equation and solve for x:

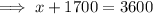
$\implies x+1700=3600$

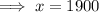
$\implies x=1900$

Therefore, Cameron made $1,900 of phone sales.

Please log in or register to add a comment.