Answer:
Approximately
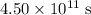 .
.
Step-by-step explanation:
The speed of light is
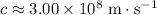 .
.
Note that the standard unit of energy, joule, is a derived unit. In terms of the standard base units:
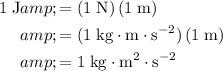 .
.
Apply unit conversion and ensure that the unit of mass is in the standard unit kilogram (
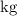 ):
):
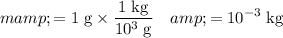 .
.
Apply the equation
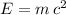 to find the energy equivalent to
to find the energy equivalent to
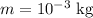 of matter:
of matter:
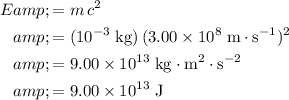 .
.
Divide energy
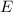 by power
by power
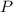 to find the duration
to find the duration
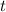 of the power consumption:
of the power consumption:
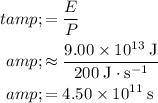 .
.
In other words, the energy equivalent to
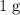 of matter could power this fridge for approximately
of matter could power this fridge for approximately
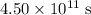 .
.