Question

PLEASE HELP!!

(04.03)
Given the function g(x) = 5(2)^x, compare the average rate of change from x = 1 to x = 2 and from x = 3 to x = 4.
How many times greater is the average rate of change from x=3 to x=4 than from x=1 to x=2?
О 4 times
O 5 times
O 2 times
O The average rate of change of Section B is not greater than the average rate of change of Section A.

Answer 1

Answer: Choice A. 4 times

========================================================

Step-by-step explanation:

We'll be using this formula

`m = (f(b)-f(a))/(b-a)`

to compute the average rate of change (AROC) from x = a to x = b. Note how this is effectively the slope formula because y = f(x).

To start things off, we'll compute the AROC from x = 1 to x = 2.

`m = (g(b)-g(a))/(b-a)\\\\m = (g(2)-g(1))/(2-1)\\\\m = (5(2)^2-5(2)^1)/(2-1)\\\\m = (10)/(1)\\\\m = 10\\\\`

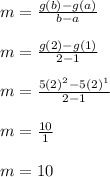
Do the same for the AROC from x = 3 to x = 4.

`m = (g(b)-g(a))/(b-a)\\\\m = (g(4)-g(3))/(4-3)\\\\m = (5(2)^4-5(2)^3)/(4-3)\\\\m = (40)/(1)\\\\m = 40\\\\`

The jump from m = 10 to m = 40 is "times 4", which is why choice A is the final answer.